What Is A Musical Interval?
Intervals are the building blocks of music.
They are a way of measuring and communicating the distance and relationship between pitches, whether they are stacked into a chord or laid out into a scale.
For example, the interval distance between A and E is larger than A and C...

Using the A - E interval as an example...
It could be expressed "horizontally", playing the notes one after the other, the basis of melody...
We'd call this a "melodic interval".
Or it could be expressed "vertically", playing the notes together, the basis of harmony...
We'd call this a "harmonic interval".
So, same interval, same musical distance, different application.
Now, while the musical alphabet names each note with a letter (A-G), intervals are represented by numbers (1-7), each one representing a specific distance between two pitches.

So the function of notes and intervals is slightly different...
While notes tell us the absolute position of a pitch on our instrument, intervals are relative to a starting or reference pitch. For example, the below table shows us how these intervals would form in relation to three starting notes (you can always come back to this table later if it looks too overwhelming right now)...
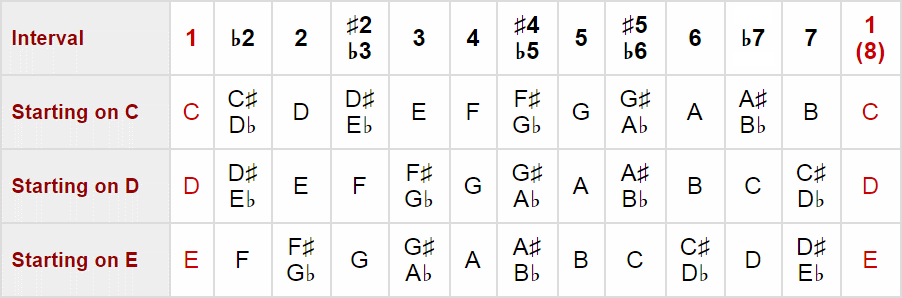
Side Note: Don't worry about whether you use a sharp (♯) or flat (♭) on a given degree right now. This will become clear as we go through this lesson. Just be aware that, in the twelve-tone (chromatic) scale, we have seven "natural" intervals (1, 2, 3, 4, 5, 6, 7) and five sharp/flat intervals (those in between the naturals).
So while C and G, for example, are two individual notes with their own names, together they represent a single interval (1 - 5) that can be positioned at different pitches.
C to G, D to A and E to B are the same interval (1 - 5), because they all represent the same distance and therefore musical relationship...
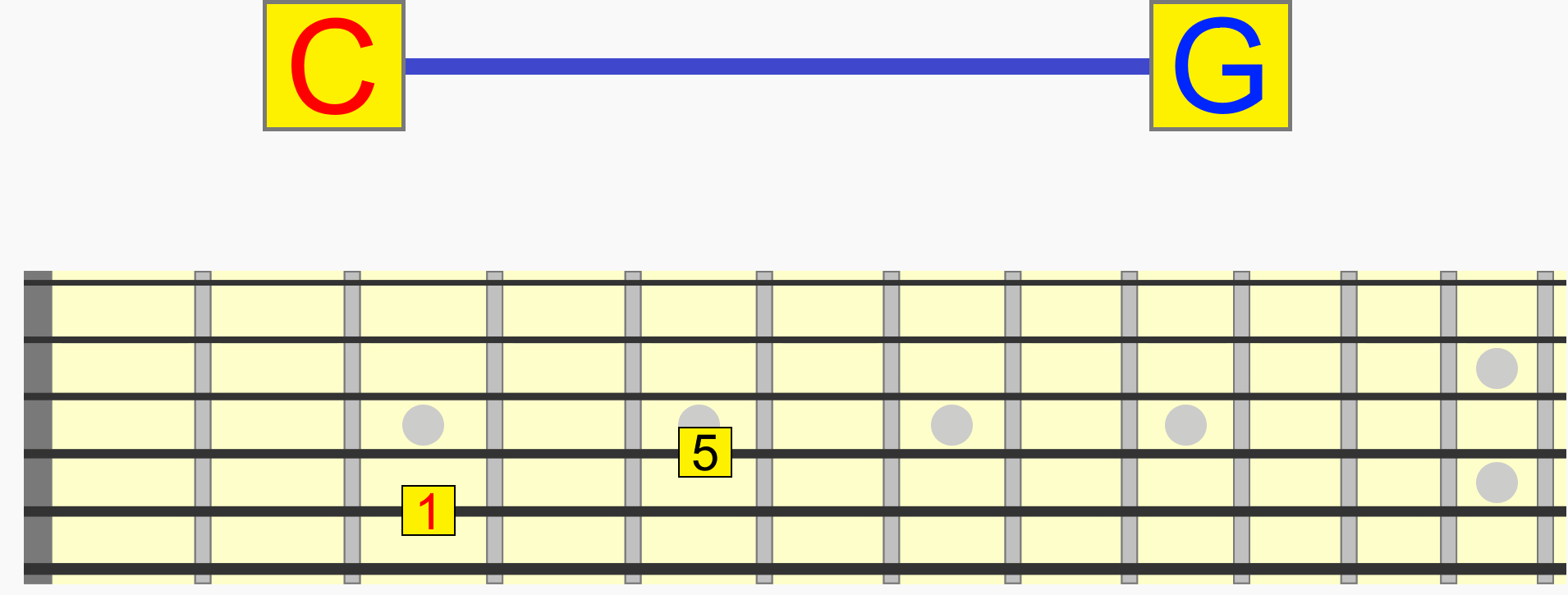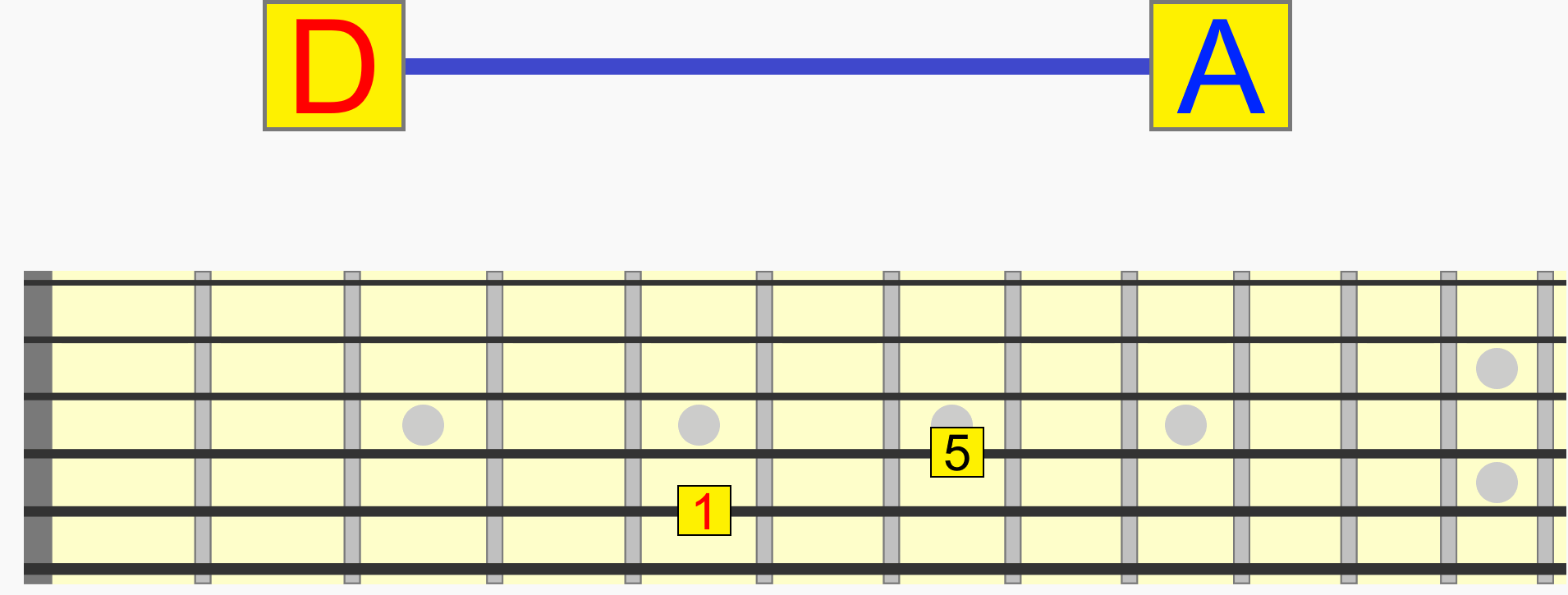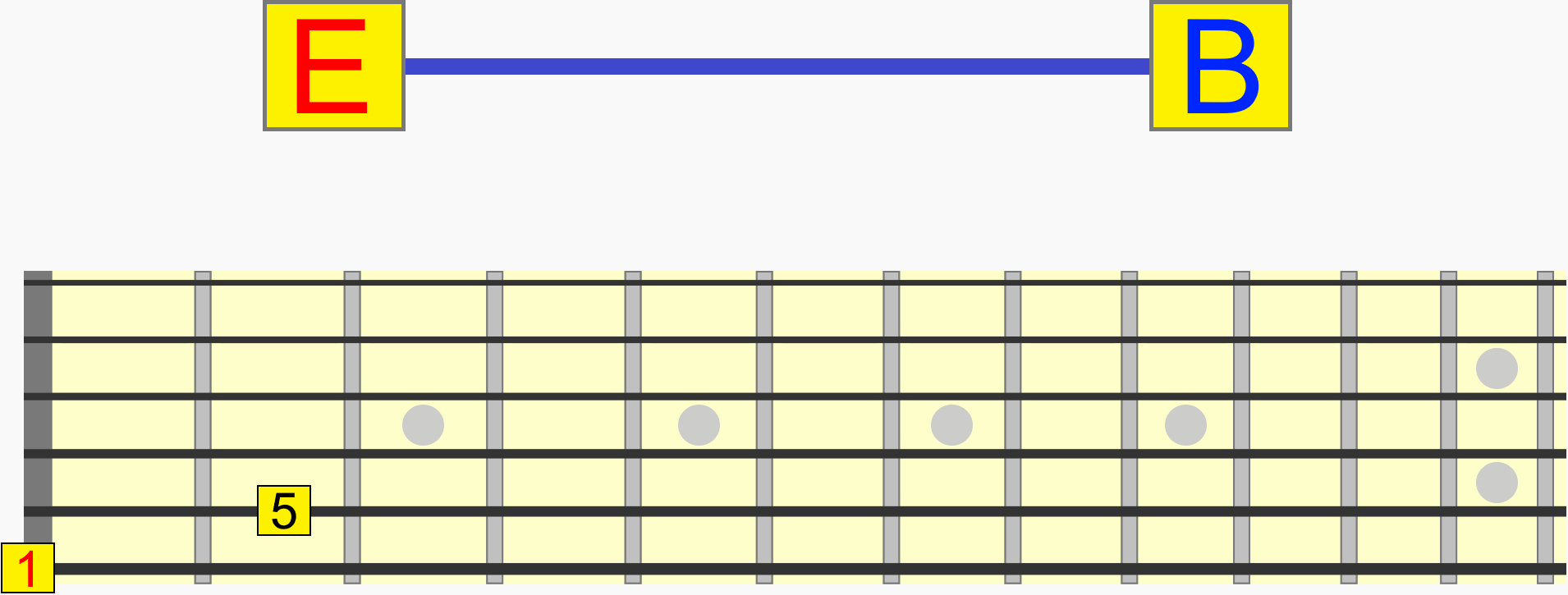
Incidentally, this interval (like other intervals) has a name - a perfect 5th. But we'll look more at naming intervals later.
Side Note: Musicians often refer to the skill of being able to identify these relationships, no matter which reference note they start on, as relative pitch recognition. Such a musician would hear the movement from E to B as the same as A to E, even though different notes are being played. It's the relationship between the notes that determines their musical quality.
You too can develop this ability using a good ear training program such as Musical U.
How Intervals Help Us Form Movable Shapes & Patterns
Visually, this ability to move relationships of notes to different places is what creates familiar shapes and patterns. Shapes for chords. Patterns for scales.
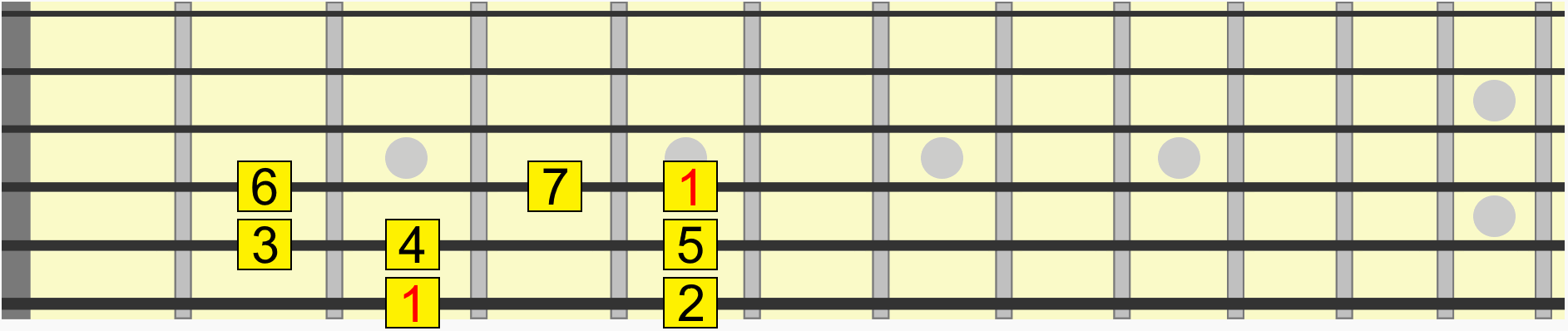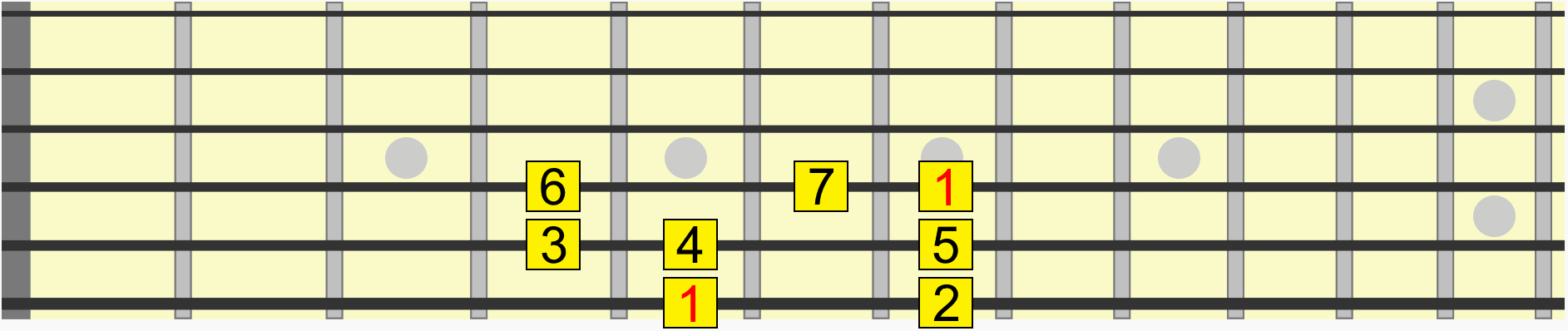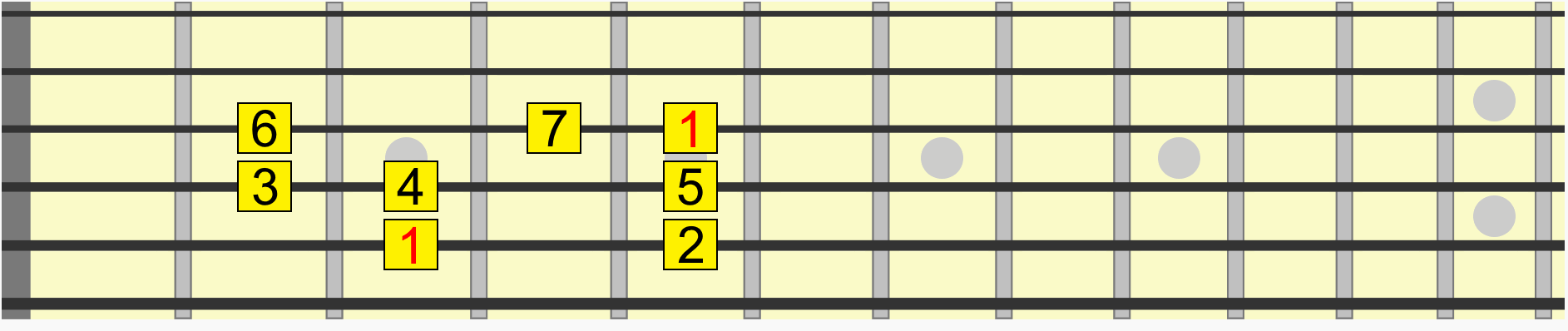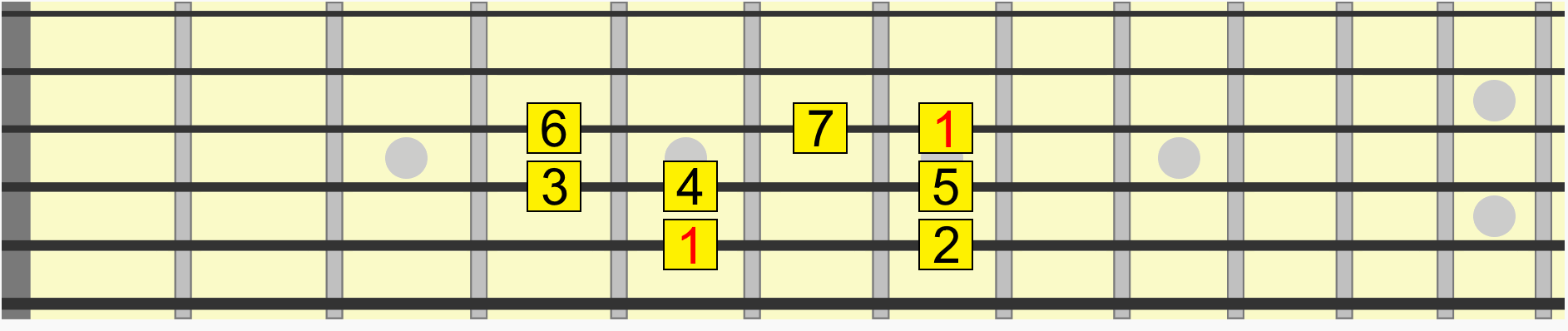
For example this scale pattern has the same interval structure whether we start it on G, A, C, D, or any starting note...
Similarly, this chord shape has the same interval structure, whether we position it on B, D, E or G...
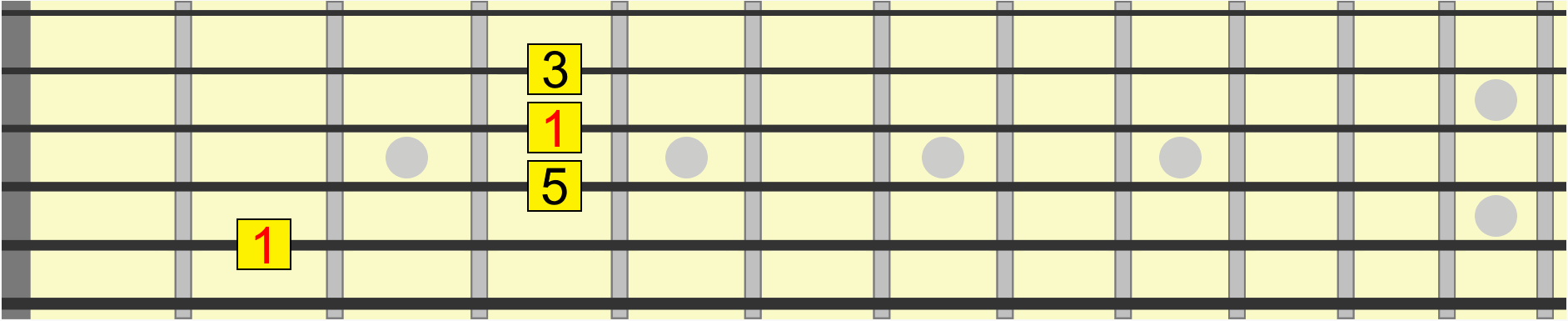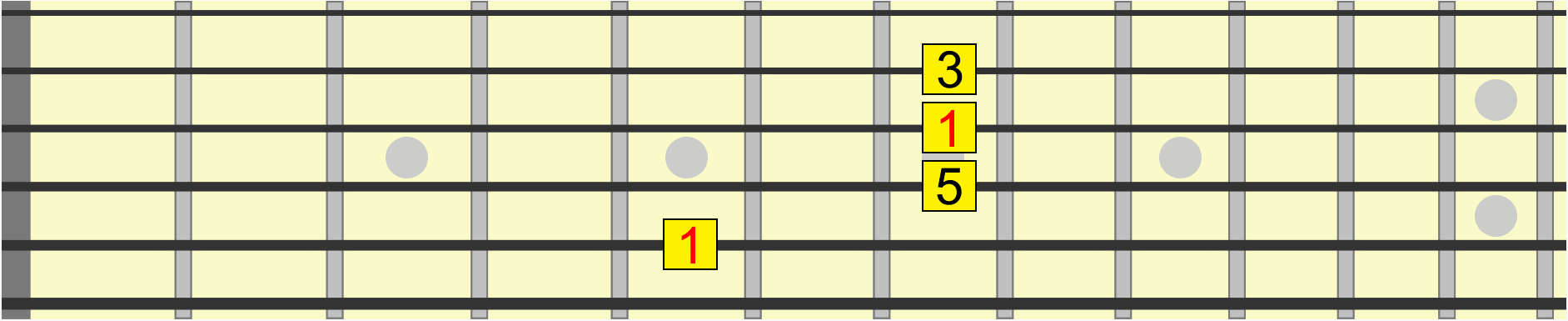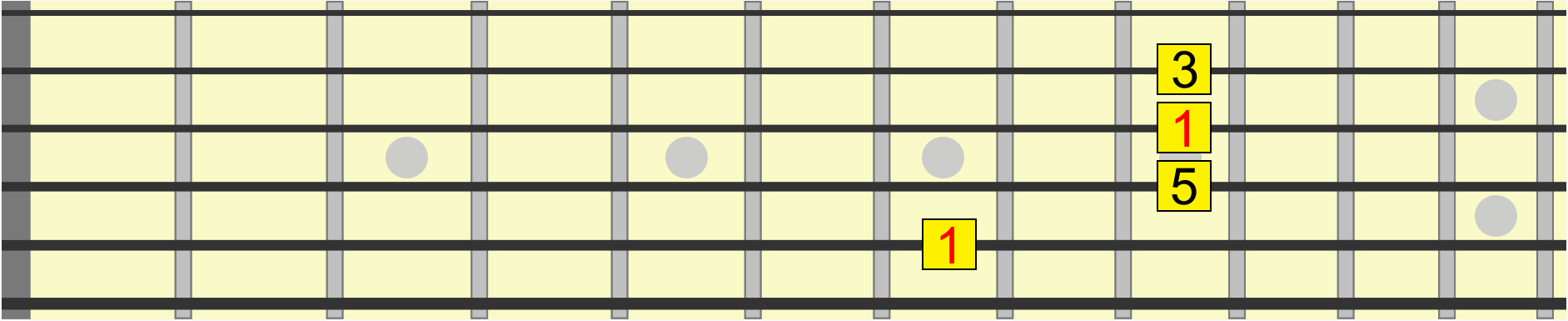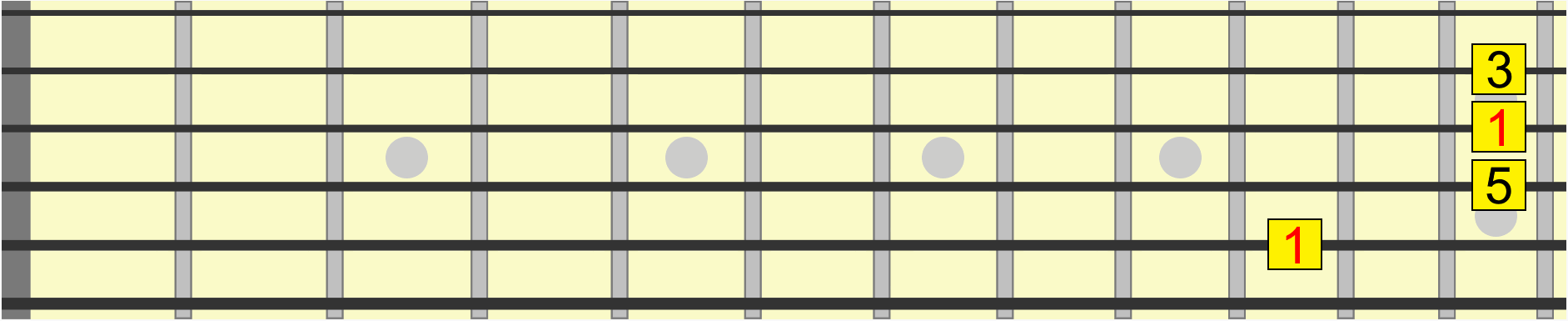
With enough practice, you'll hear the shape on B as the same as the shape on E, even though the second one is collectively higher in pitch. In other words, both positions share the same musical quality.
Back to our scale pattern. Contained within it are several pitches and therefore several intervals in relation to a starting or reference pitch, sometimes called the root or 1.
Using the first instance of the root, see how on the animated diagram we move through each interval in the scale from its 1st to 7th degree.
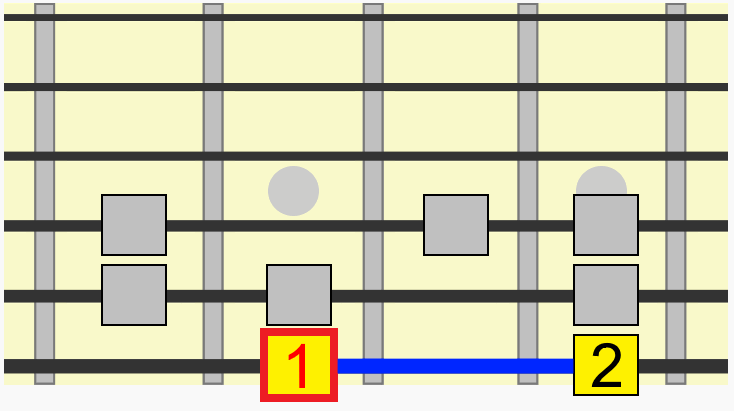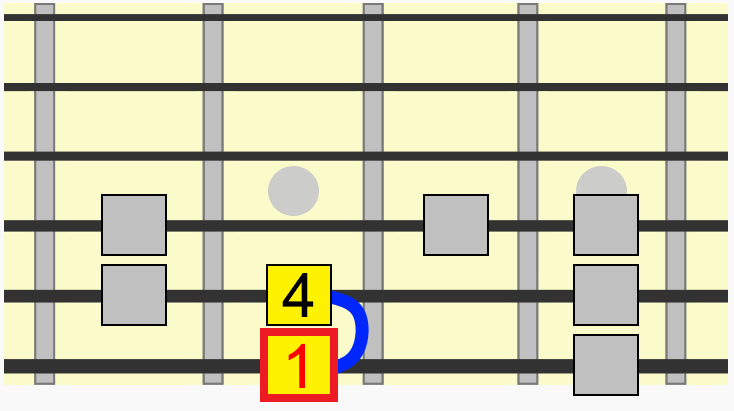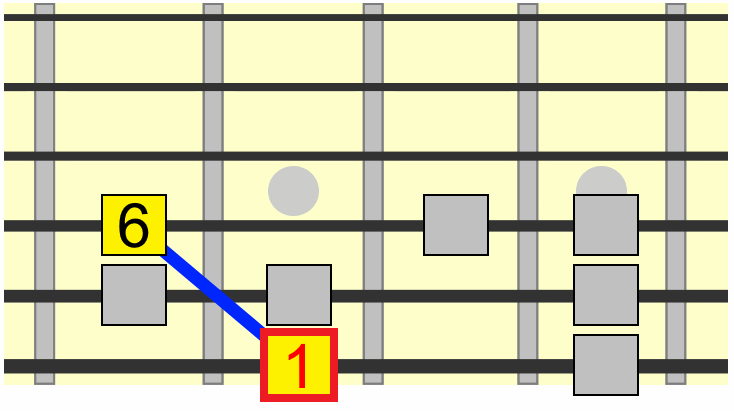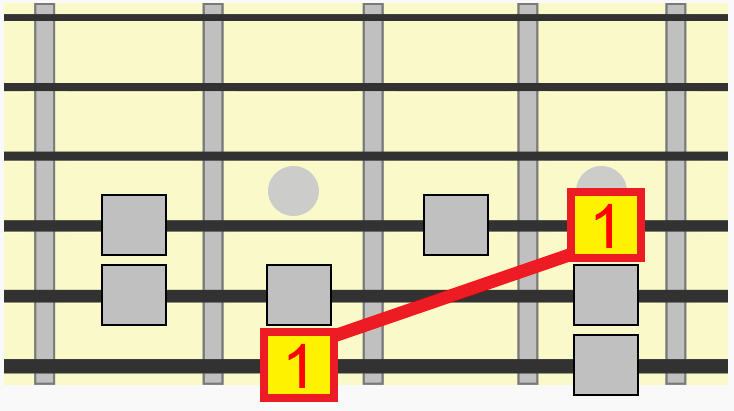
Let's take just one interval from that pattern, between its 1st and 3rd tone, more accurately called the 1st and 3rd degrees of the scale.
By training your eyes and ears to identify this relationship, we can target that same interval in any position or key. 1st to 3rd.
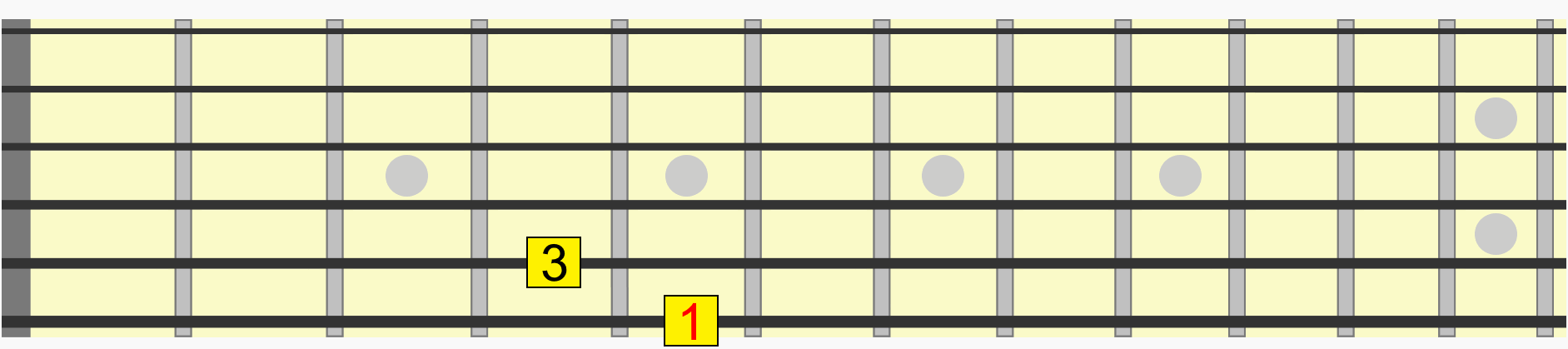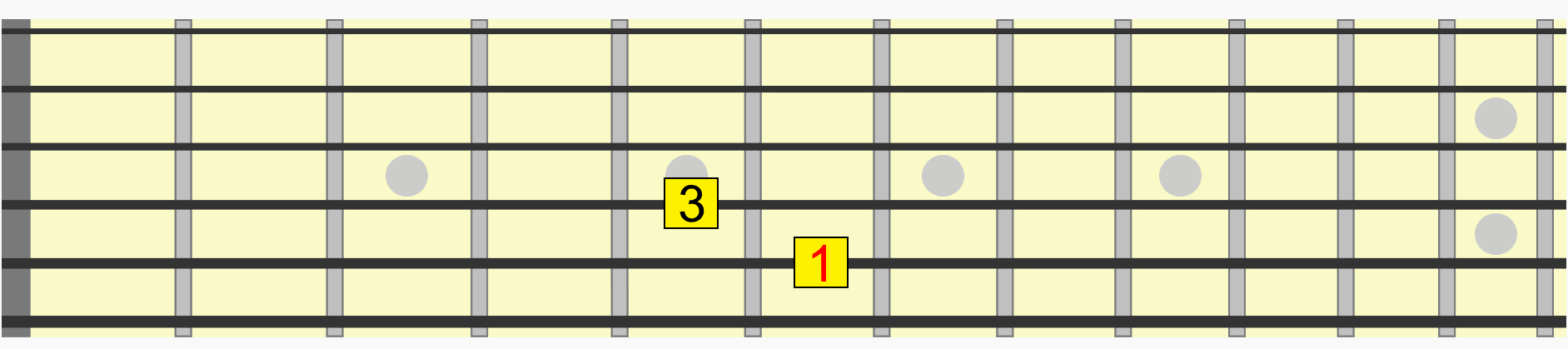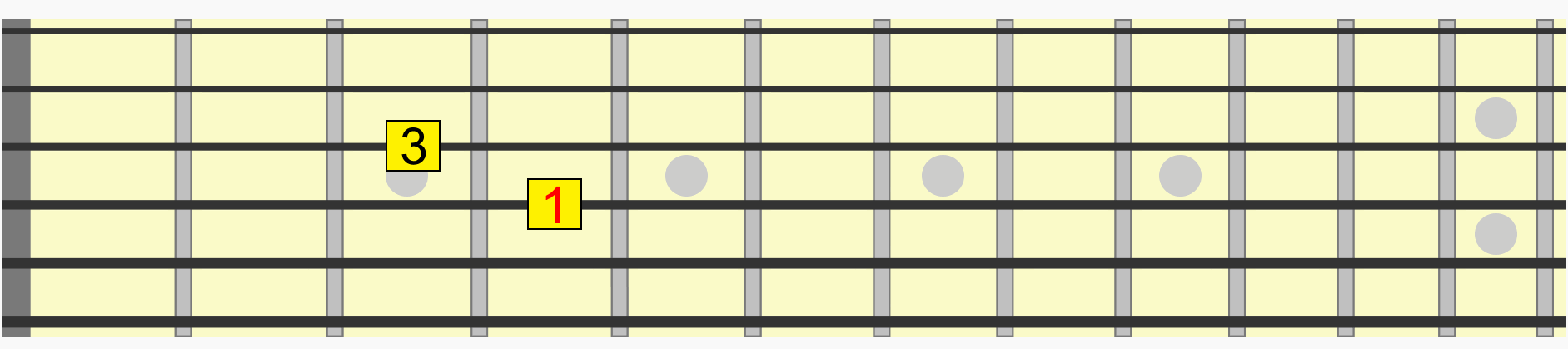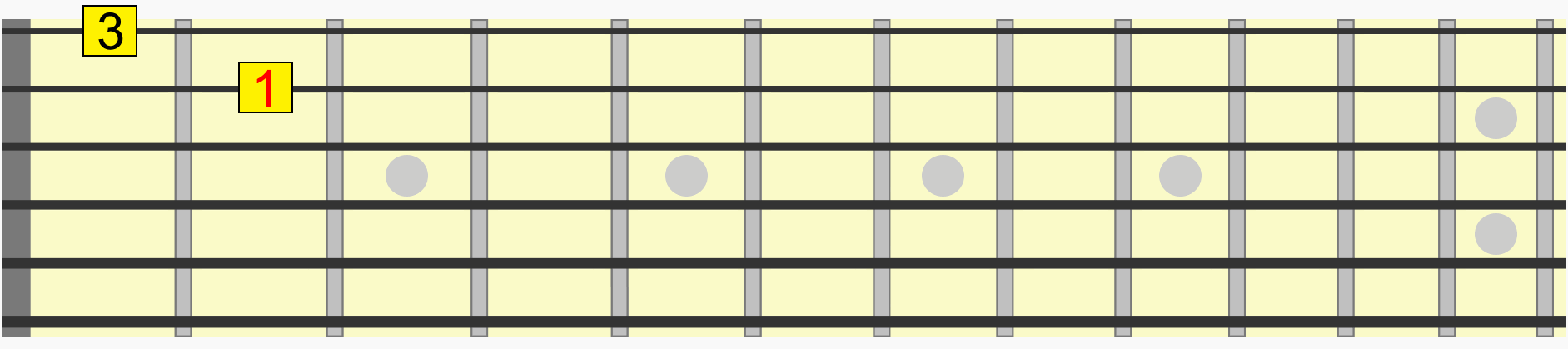
Notice how we didn't even need to think about which alphabetical note we were moving to in each position. We just used the familiarity of the visual and aural relationship of the interval to recreate it in a new position.
Extend this concept to entire patterns or shapes (as we will do throughout our learning journey), and you should be able to see the benefit that intervals give us in forming familiar movable relationships across the neck, no matter which key we may be playing in.
Numbering & Naming Intervals
While many musicians identify intervals based purely on sight and sound, most find it useful to also label these intervals using numbers. This also helps to communicate what's going on with other musicians. You'll see these numbers being used in most of the diagrams in my (and other teachers') lessons. So let's find out where they come from.
Going back to our scale pattern...
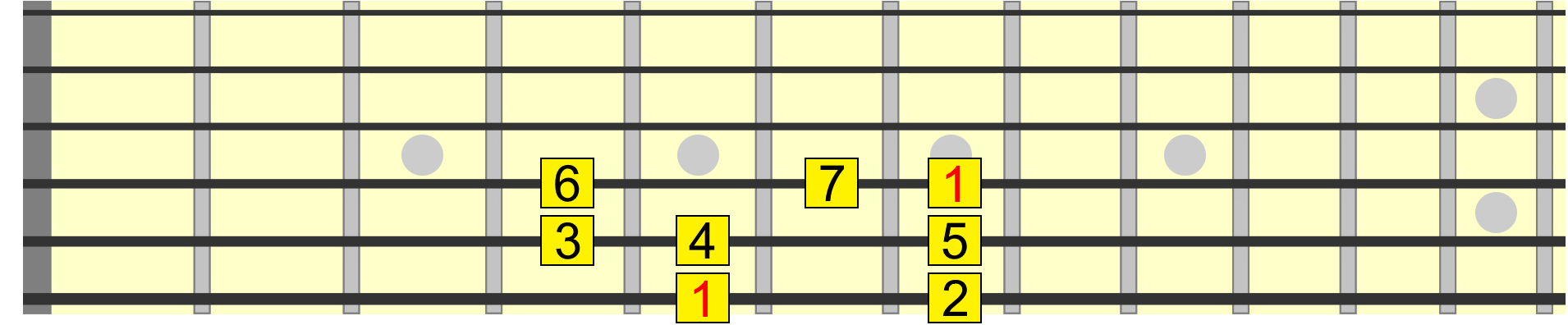
- We can label its first degree as 1 - the root and therefore reference for all the other intervals in the scale.
- Second degree, we can label this 2, also called a major 2nd interval.
- Third degree, we can label this 3, also called a major 3rd interval.
- Fourth degree, 4 also known as a perfect 4th.
- Fifth degree, 5 or perfect 5th.
- Sixth degree, 6 or major 6th.
- and 7th degree, 7 or major 7th.
We now arrive at the octave of the root - the same note and scale degree as the 1. Some musicians prefer to label the octave as 8. But I think it's less confusing to just use 1 at each occurrence of the root.
So, seven degrees in total and therefore seven intervals in relation to the root, which is A in the above diagram.
Incidentally, this scale has a name. It's most commonly known as the major scale. Since the 1 is on A, we call it the A major scale. So the root determines which letter we use in the scale name. If the root was on C, for example, and we used the same interval structure, we'd have the C major scale.
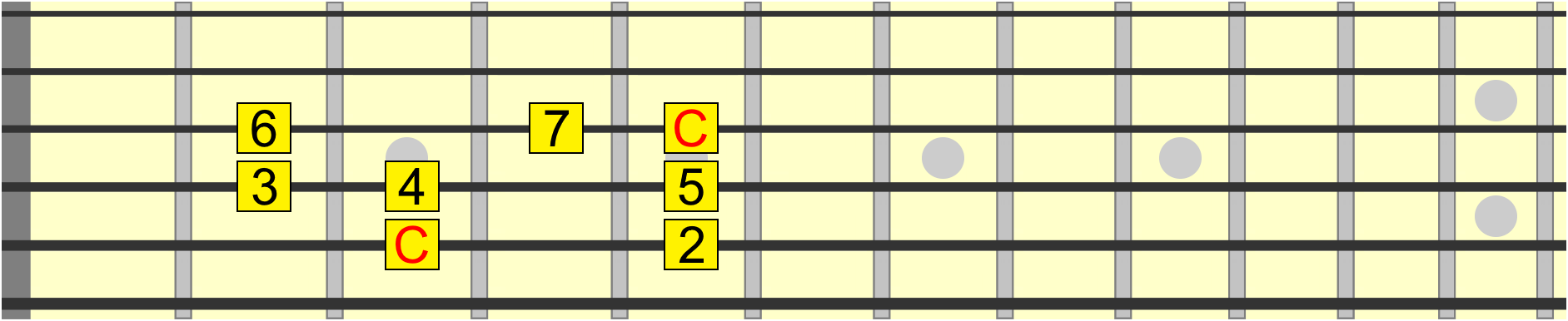
Therefore, it's the interval structure that determines the name we give to the scale after the root note.
Now, those who are just starting out with all this might confuse degree numbers with interval numbers. For example, if we take out the 4th and 7th from the major scale, we now only have five degrees, also known as a pentatonic scale...
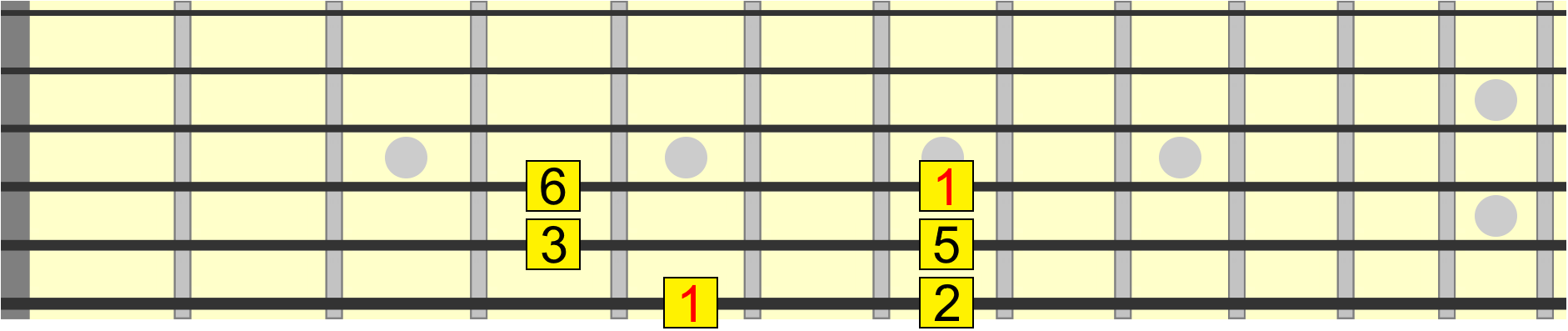
But we still use the same interval numbers on those remaining degrees - 2 3 5 and 6, because these represent specific positions or distances in relation to the root.
Just saying a scale has five degrees doesn't tell us much about its musical structure. But if we say it has a 2, 3, 5 and 6, that tells us something very specific about its structure. It tells us the position of each degree in the scale in relation to the 1.
Let's go back to our seven-tone (heptatonic) major scale.
What would happen if we moved the second degree down by one fret or semitone?
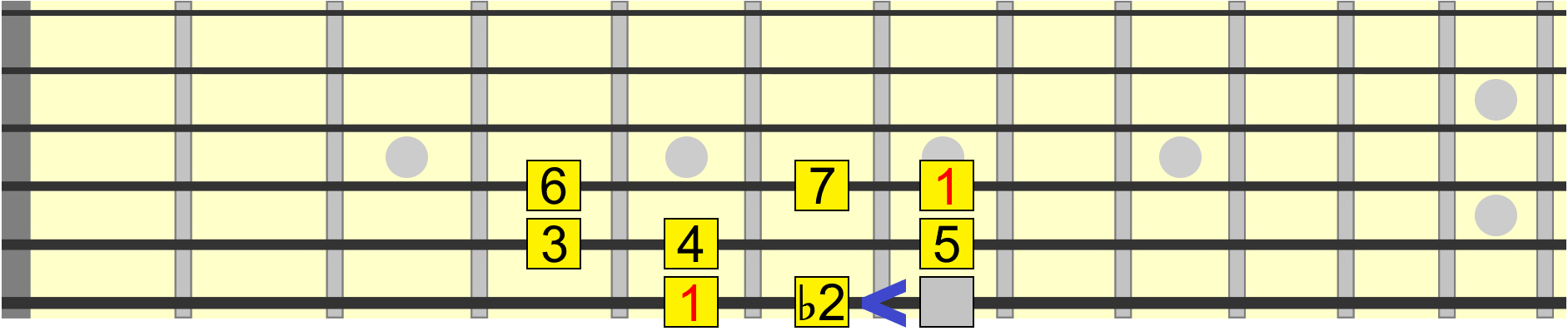
Now the scale has a flat 2nd. Also called a minor 2nd. So we had a major 2nd interval before, and now we've lowered it to a minor 2nd interval. This is the smallest interval that exists on a regular, fretted guitar.
So there's just one fret or semitone between the 1 and ♭2. You should play these intervals as we go to help train your ear to their sound.
Even though we've only changed one interval, it gives the scale quite a different sound, along with a unique name (don't worry too much about that now - we'll explore individual scales in their own lessons).
However you describe that sound, its useful to know what creates it. With enough practice, you'll be able to hear the minor 2nd's presence in a melodic sequence. But that comes with exploring scales individually.
Let's put the 2 back in its original position. You could call this its "natural" position, since it's not sharp or flat.
What if we moved the 3rd in the same way?
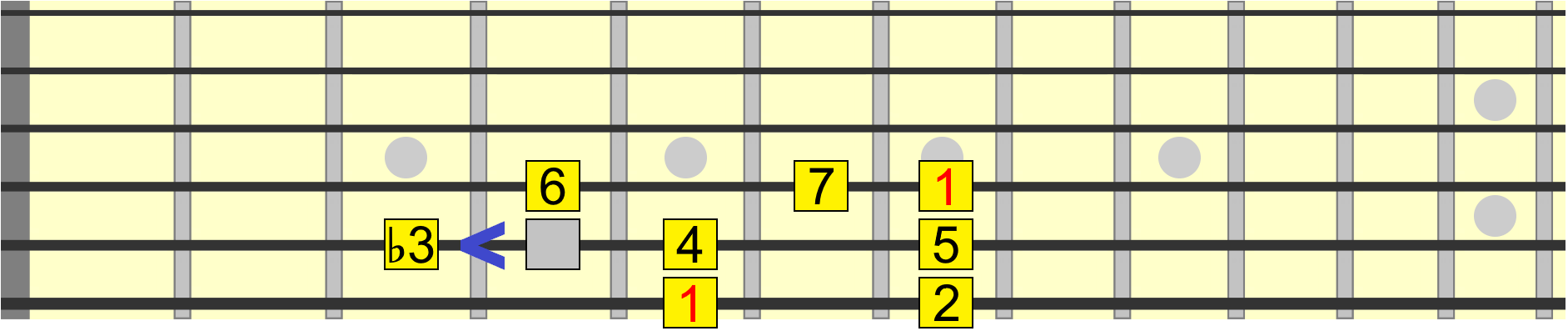
Predictably, we get a flat 3rd also called a minor 3rd, a key interval in minor chords and scales. Like the minor 2nd, the minor 3rd gives the scale a specific quality when played with the other intervals.
We've now turned our major scale into a minor scale. And all because of one small interval change on the 3rd degree. We could, if we wanted, play the minor 3rd on the sixth string instead, since it represents the same note and distance from the 1...
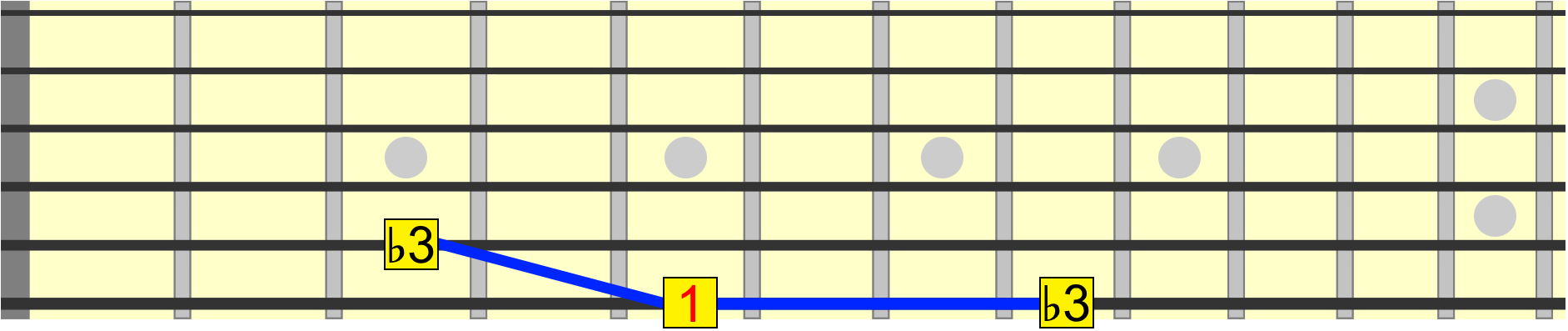
Back to major. Let's now move the 4th degree. We can't move it down because the 3rd is there...
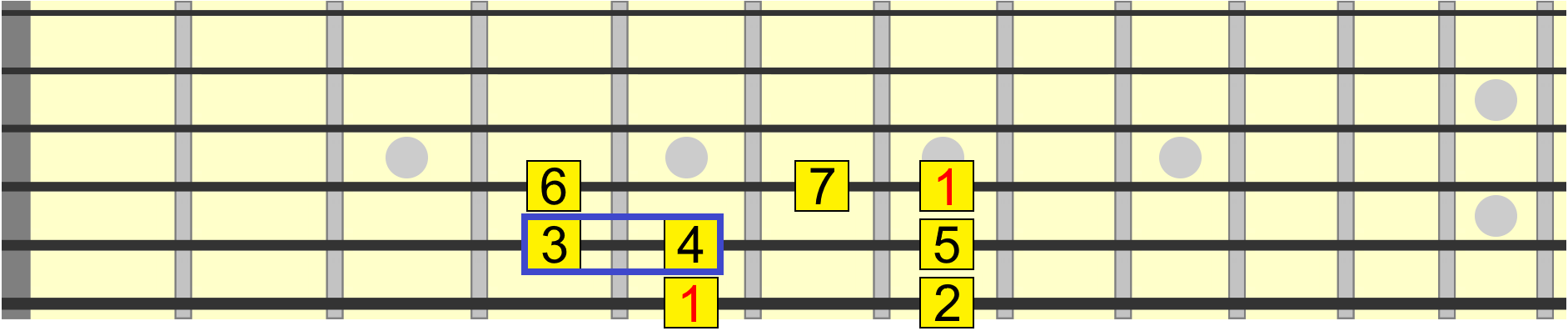
So let's move it up instead!
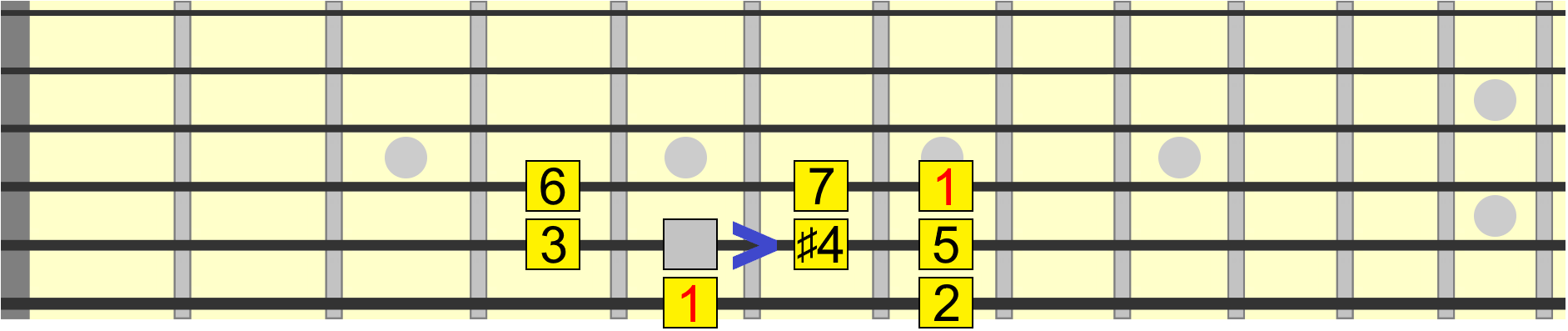
Now we have a sharp 4th, also called an augmented 4th. Why augmented? A historically used term for the sharp 4th that you can read about if you're interested.
Just remember that augment in music is interval speak for sharp.
Like the other interval changes we made, this augmented 4th creates a new scale with a unique sound.
Side Note: As we go through these changes, you can pick out certain visual relationships between the interval positions. For example, the #4 is one fret or semitone down from the 5th. This is the case no matter where the scale is played. In other words, these relationships are movable.
We don't even need to know the note it's positioned on. Intervals are about relative positions.
Back to the original position, let's now move the 5th. Now, here's where things can get a little confusing. We can potentially have a flat 5 or a sharp 5...
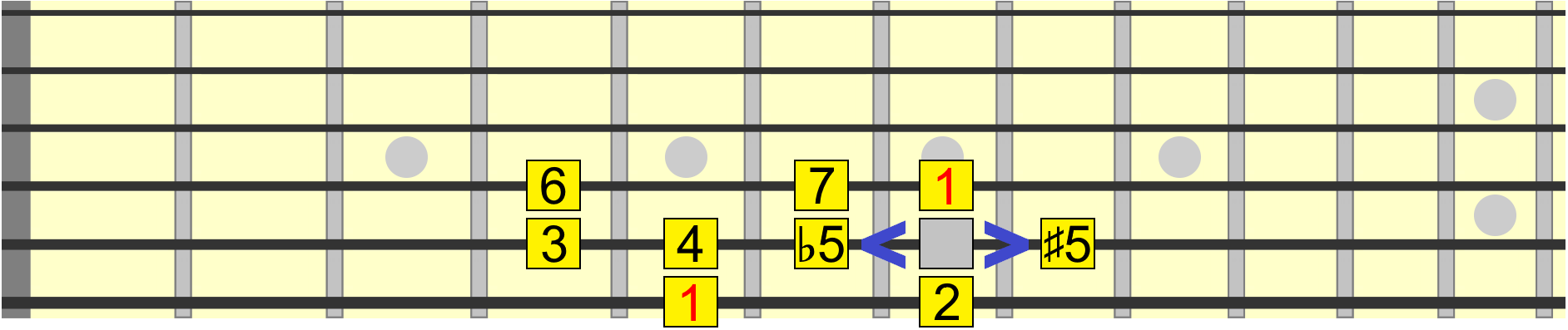
A flat 5, also known as a diminished 5th, occupies the same position as an augmented 4th! So how do we know whether to call it a 5th or a 4th? Well, if there's already a 4 in the scale, we use a ♭5.
You'll see the ♭5 used in scales such as the one below, along with a minor 2nd and minor 3rd. As there's a 4 in this scale, we use a diminished 5th instead of an augmented 4th...
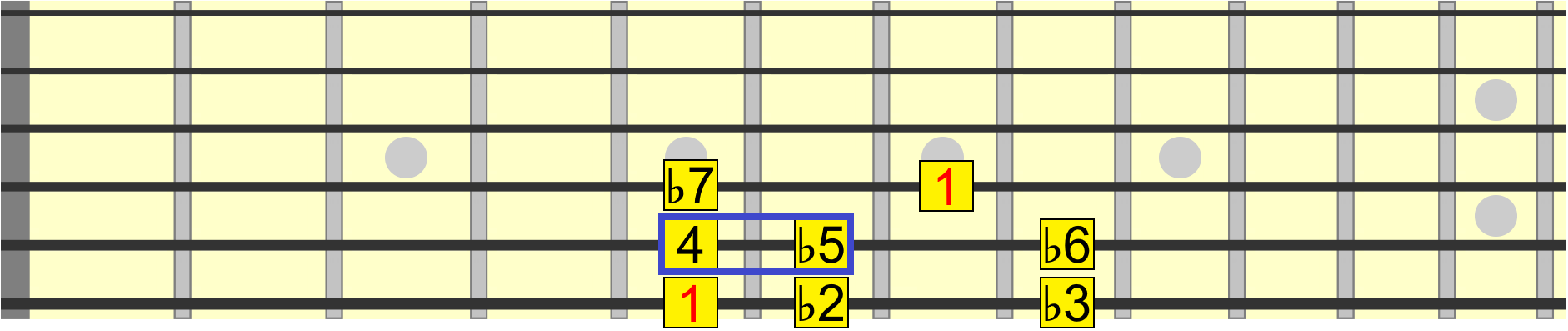
Side Note: When two intervals share the same pitch like this, such as the augmented 4th and diminished 5th, they are known as enharmonic. It's the presence of other intervals that determines which one we use.
Wherever possible, a seven degree scale should be numbered from 1 to 7, with the appropriate flats and sharps indicated where necessary.
We could also raise the 5th, giving us a sharp 5, also known as an augmented 5th...
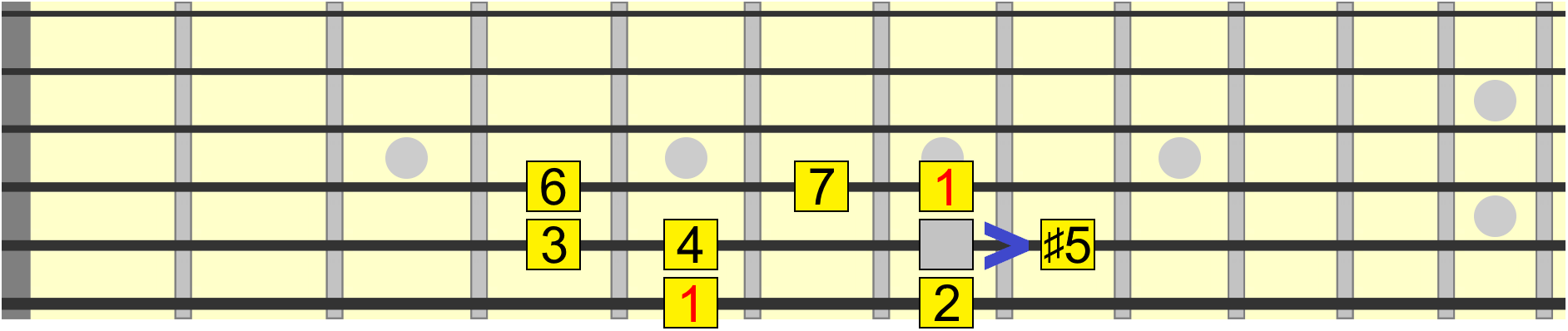
But based on the numbering rule we just established, if there's already a 5 in the scale, the sharp 5 position becomes a flat 6, or minor 6th. For example, you'll hear the minor 6th being used in scales such as harmonic minor...
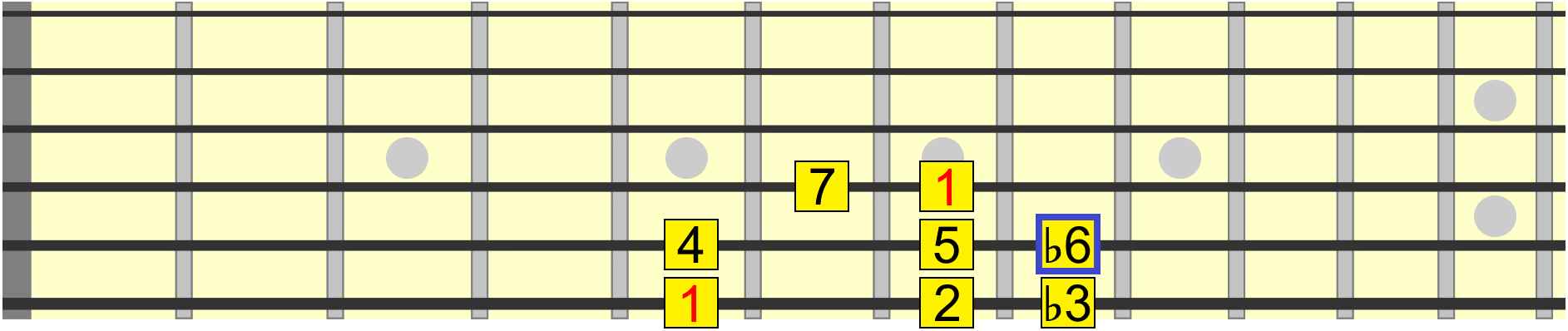
Finally, the 7th degree, which can either be a major 7th, simply numbered 7, or a minor 7th when in its flat position. The minor 7th shows up in several minor scales and major scales like Mixolydian, which is simply the major scale with a ♭7...
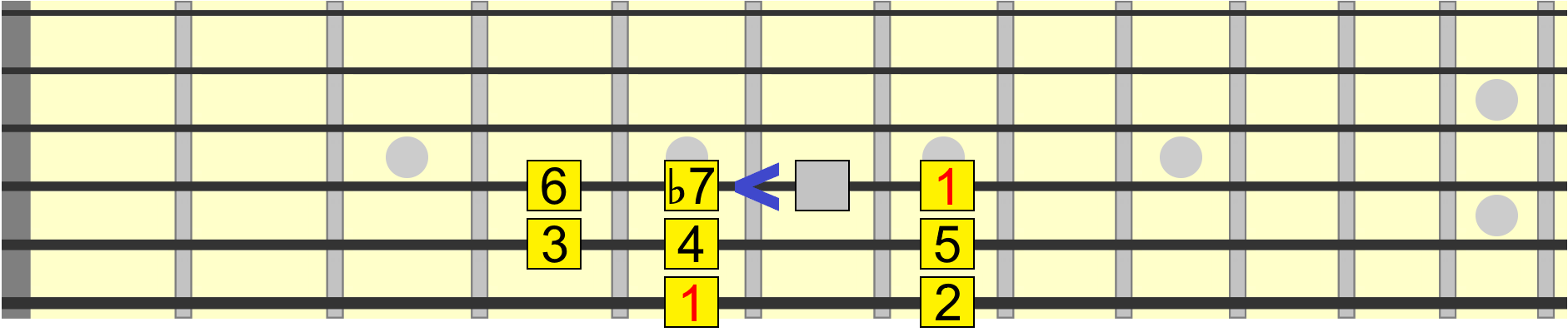
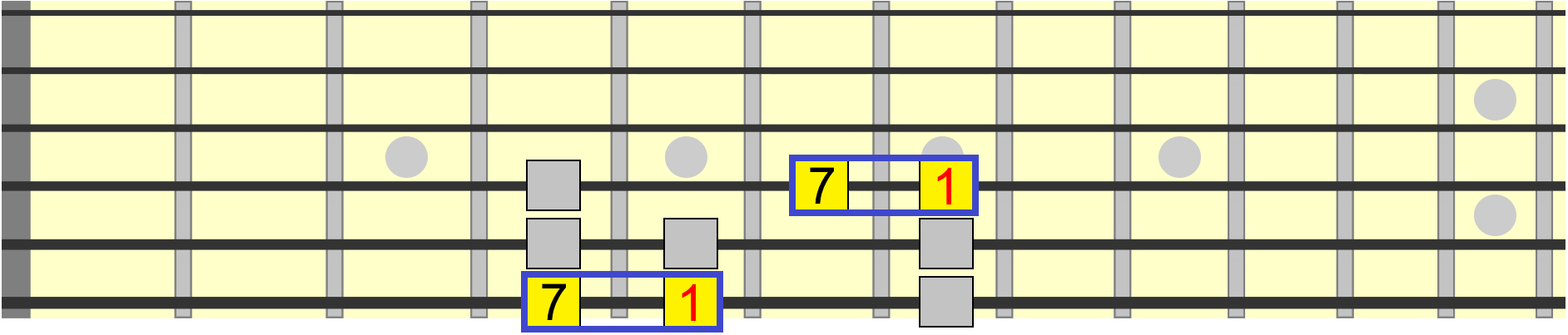
One visual cue for identifying the major 7th is one fret down (one semitone) from the root. Therefore we could also position a major 7th on the 6th string as shown...
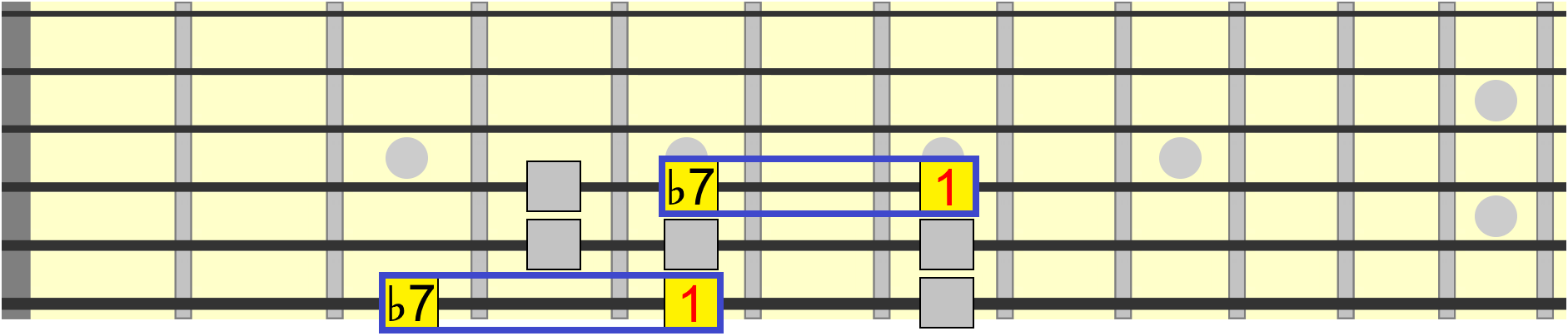
A minor 7th is always two frets (a whole step) down from the root...
The Practical Function of Intervals
It's the different combinations of these intervals, whether natural, flat or sharp, that give us the different scale qualities we need to play over compatible chords and progressions.
For example, if the chord we're playing over is minor, we'll know that a minor 3rd interval will be a part of the scale...
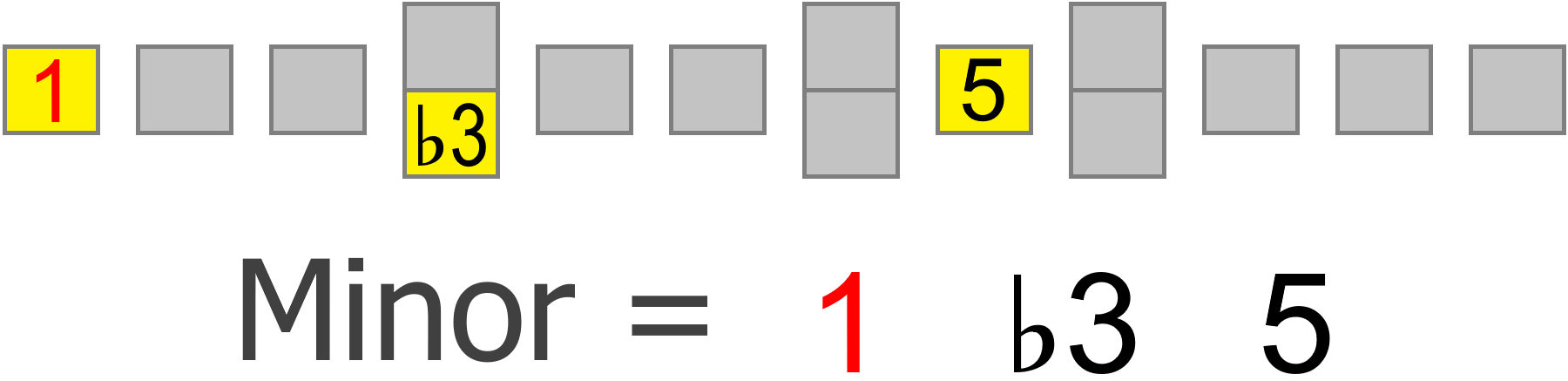
If the chord has a minor 7th, we'll want to ensure our scale matches that...
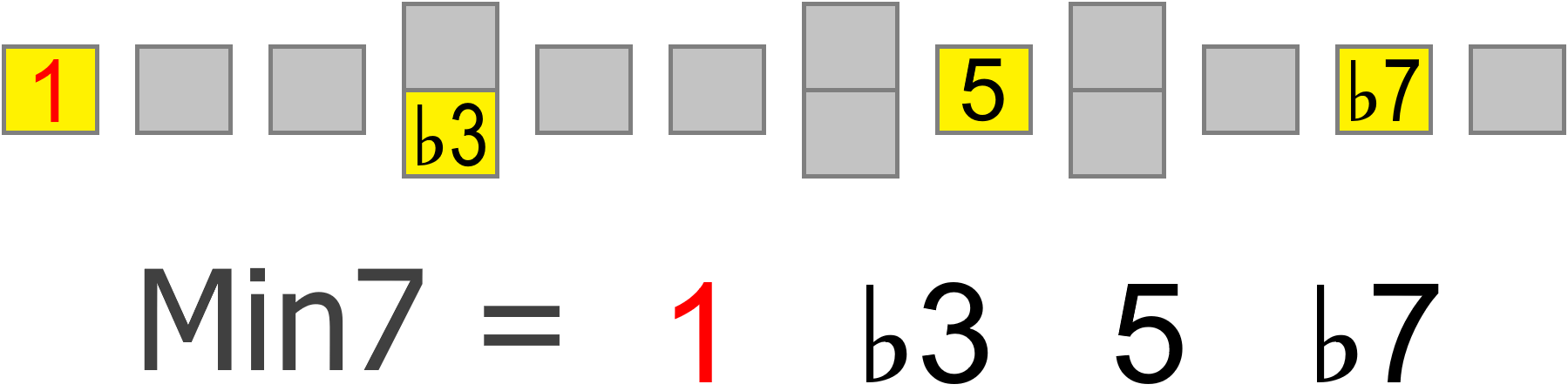
But more importantly, intervals specify the pitch of each scale degree, no matter where the root of that scale is positioned on the neck.
So while an A minor scale uses different notes to a D minor scale, the only notes we really need to be aware of are the roots, since the interval structure of the scale is the same for both.
Whether the minor scale starts on A, B, C, D, E etc. its interval structure is still 1 2 ♭3 4 5 ♭6 ♭7. The relative distance between each pitch in the scale is the same on any root...
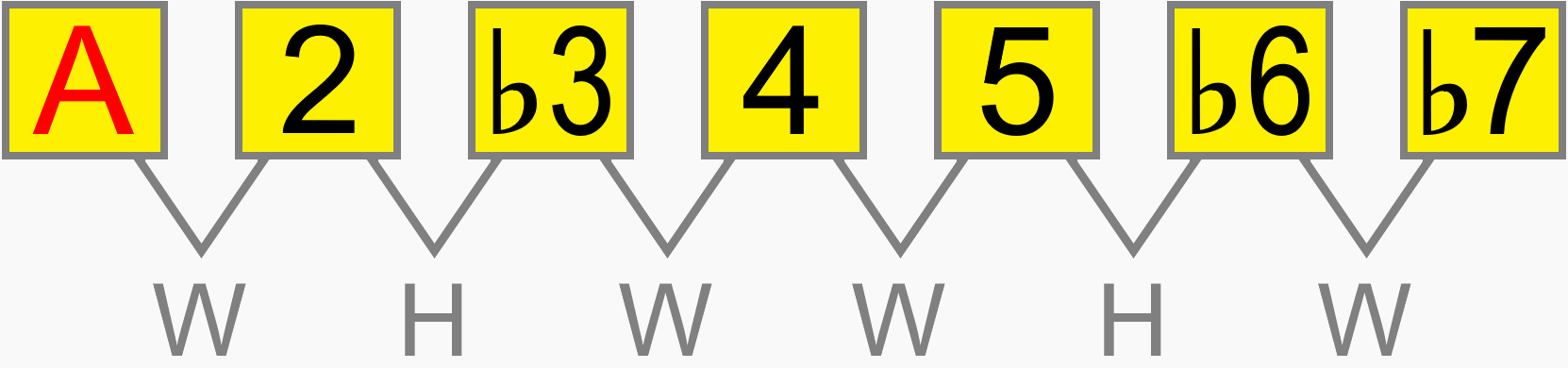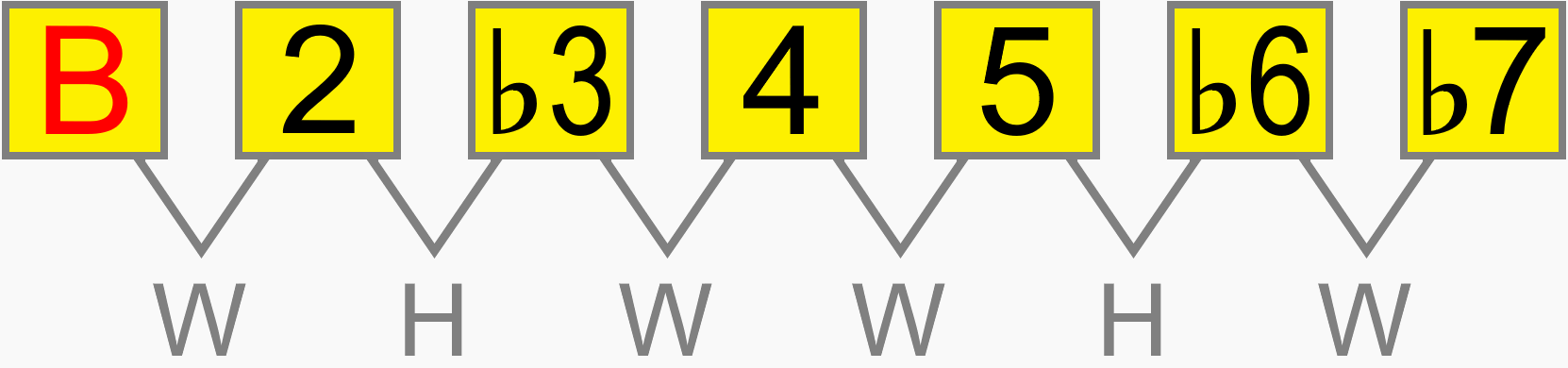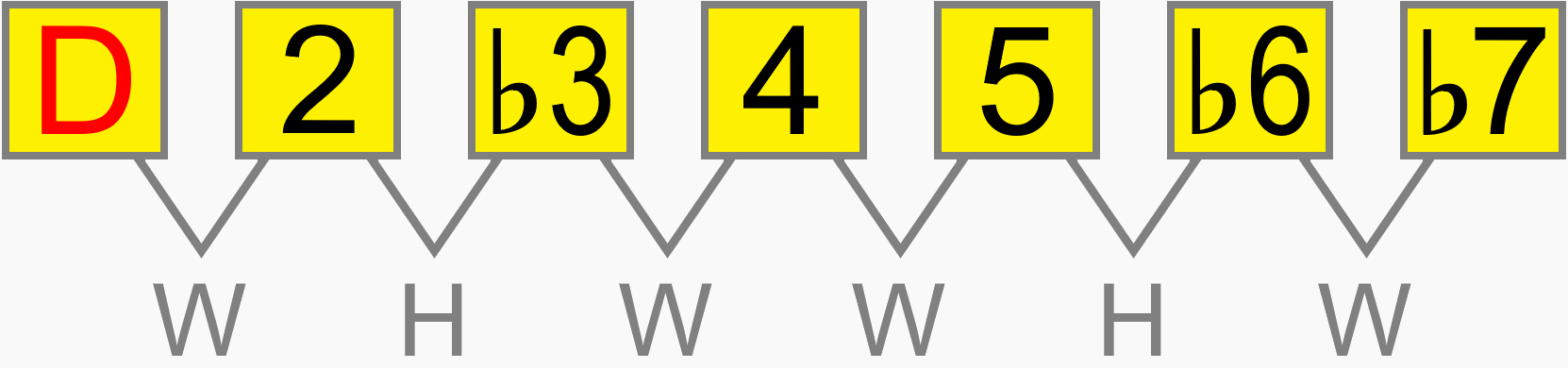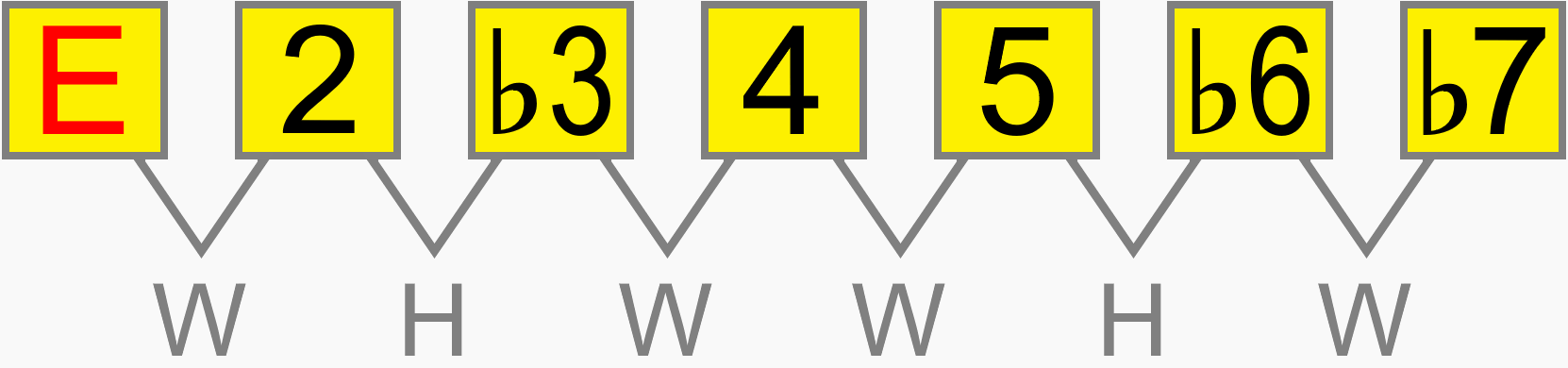
Eventually, you'll be able to work out how a scale would be formed on the neck, simply by its numbering formula. For example, 1 ♭2 3 4 5 ♭6 ♭7 gives us this scale, known as phrygian dominant...
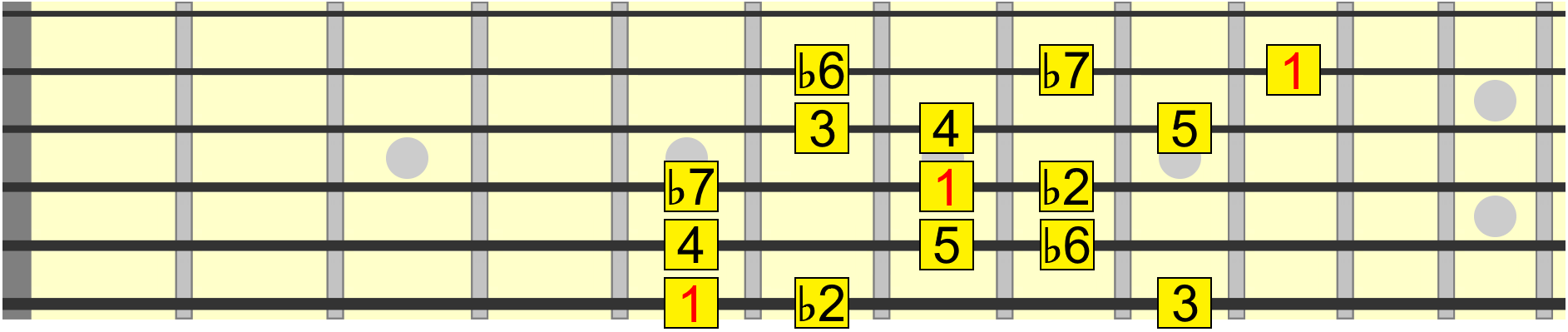
See if you can add in the correct interval positions on the 1st string.
The benefit of knowing where each interval in a pattern lies is that you can target specific intervals in your phrases for the sound you want. For example, you might want to target the 3 of the scale. Or, for a more tense sound, you might target the ♭2. More on that another time.
Intervals At A Glance
The below table takes us through each interval, including its half/whole step formula and an audio example of it being played using a C reference (so C is 1 in each example). Each interval represents a specific musical distance and therefore sound.
| Interval | Interval Name | Half/Whole Step Space | Hear It |
| 1 | Perfect Unison | - | - |
| ♭2 | Minor Second | H | |
| 2 | Major Second | W | |
| ♯2 ♭3 |
Augmented Second Minor Third |
W H | |
| 3 | Major Third | W W | |
| 4 | Perfect Fourth | W W H | |
| ♯4 ♭5 |
Augmented Fourth Diminished Fifth |
W W W | |
| 5 | Perfect Fifth | W W W H | |
| ♯5 ♭6 |
Augmented Fifth Minor Sixth |
W W W W | |
| 6 | Major Sixth | W W W W H | |
| ♭7 | Minor Seventh | W W W W W | |
| 7 | Major Seventh | W W W W W H |
As you progress through my lessons, the numbers I use in the diagrams should now be familiar to you. But what's really powerful about becoming "interval literate" is that you'll start to see and hear movements across the neck in relative terms, rather than just a bunch of notes.
Practically, this means you'll be able to recreate the sound you want (based on the intervals from which it is built) in any place on the neck. This skill will evolve as you learn more about the application of melody and harmony.
If you want more in depth help with unlocking the powerful skill of recognising intervals by ear, I highly recommend Musical U's ear training program.
